一般的なプリミティブまたは特に部分的なプリミティブを計算するための式は、学生がよく遭遇する数学の解決策の 1 つです。によるこの記事では、すべてのタイプの部分原始問題の公式と解決策をまとめます。
目次
原始関数とは?部分プリミティブとは
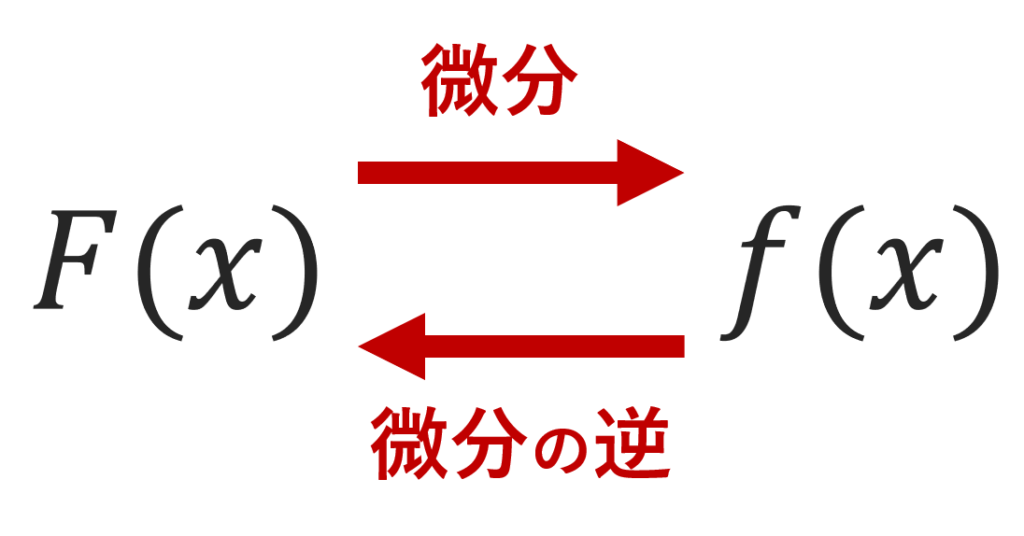
数学、特に微積分 (代数としても知られる) では、与えられた実関数 f の原始関数は関数 F であり、導関数は f、つまり F’ = f です。プリミティブを見つけるプロセスは、不定積分と呼ばれます。
そして、プリミティブの式を見つけることは、導関数を見つけることよりも難しくなり、時にはそれが不可能になることもあります. ただし、a から b までの区間または範囲で連続する任意の関数には、上記の a から b までの区間または範囲でその関数のプリミティブが存在します。
部分プリミティブとは
部分原始法は、複雑な関数の不定積分を求めるためによく使用されます。つまり、無理関数、対数関数、指数関数、関数、三角関数など、多くの種類の関数を 1 つの計算に組み合わせるために使用されます。
基本的な部分プリミティブの式
2 つの関数 u = u(x) と v = v(x) が K の連続導関数で与えられると、部分原始式 ∫udv = uv−∫vdu が得られます。
注: プリミティブが I=∫f(x).g(x)dx の形式の場合、部分プリミティブ法をよく使用します。ここで、f(x) と g(x) は 4 つの関数のうちの 2 つです: 対数関数、多項式関数、三角関数、指数関数。
∫f(x).g(x)dx の部分プリミティブを計算する手順
ステップ 1:設定する
最も完全な部分原始式
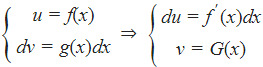
ここで、G(x) は関数 g(x) の任意のプリミティブです。
ステップ 2:次に、部分原始式によると、次のようになります。
∫f(x).g(x)dx=f(x).G(x)−∫G(x).f'(x)dx.
注: I=∫f(x).g(x)dx と f(x) と g(x) が 4 つの関数の 2 である場合: 対数関数、多項式関数、三角関数、規則に従って設定した関数関数ハットuを配置する。
- 最初のログ (関数ログ、ln) – 2 番目のポリ (多項式関数)
- Trigonometric (三角関数) – Quadratic (指数)
つまり、上記の文で最初に来る関数が何であれ、u をその関数に等しく設定します。次のように:
- f(x) が対数関数で、g(x) が残りの 3 つの関数のいずれかである場合、次のようになります。
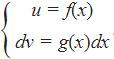
- 同様に、f(x) が指数関数で g(x) が多項式関数の場合、次のようになります。
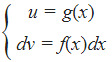
部分原始式を適用したサンプル演習
上記の式を実践的な演習に簡単に適用する。 は、次の部分プリミティブ式を基本から上級まで適用するいくつかの問題を紹介したいと思います。
部分プリミティブ問題の一般的なタイプ
サンプル問題や公式試験問題で見つけやすい4種類の部分原始問題です。
部分プリミティブをすばやく計算するためのヒント
上記の基本的な部分プリミティブ計算に加えて、次のように対角法を計算に適用することもできます
フォーム 4: 反復プリミティブ (反復積分)
対角線図に従ってプリミティブ (積分) を計算するときに、計算する元のプリミティブを (水平方向の行で) 繰り返すと、常にその行で停止し、計算を続行しません。
- 停止時の符号: 同じ行で、2 列の 2 つの要素の積 (符号と係数を除く) が、計算される元のプリミティブと同じであることに注意してください。
- 上記の例のように結果を記録します (斜めに掛けます)。
- 2 つの要素を (ストップ ラインで) 結合し、結果の前に記号を追加し、ハイフンを対角線として扱い、編み方規則を使用します。
つまり、知識を覚えるだけでなく、部分的な原始的な問題を解決する方法を習得することができます. さまざまな種類の数学の問題を解くには、もっと練習する必要があります。
