この記事では、算数 面積 問題 難しいについて明確にします。 算数 面積 問題 難しいを探している場合は、この【受験算数の面積問題】発想力が問われるちょっと難しい図形の問題!の記事でComputer Science Metricsを議論しましょう。
目次
【受験算数の面積問題】発想力が問われるちょっと難しい図形の問題!の算数 面積 問題 難しいに関する関連情報の概要最も正確
このComputerScienceMetricsウェブサイトでは、算数 面積 問題 難しい以外の知識を追加して、より価値のある理解を深めることができます。 csmetrics.orgページで、私たちは常にあなたのために毎日新しい正確なニュースを更新します、 あなたに最も完全な知識を提供したいという願望を持って。 ユーザーが最も完全な方法でインターネット上の理解を更新することができます。
算数 面積 問題 難しいに関連する情報
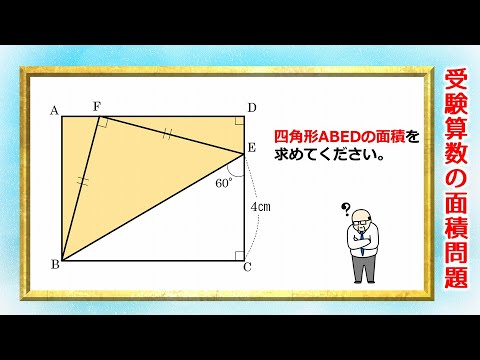
#面積の算数問題 #難問 #良問 「長方形ABCDでFB=FE、EC=4cm、∠BEC=60°のときの四角形ABEDの面積を求めよ。」 必要とされている。 パズルのように考えることをお勧めします。 暇つぶしに是非お立ち寄りください! ==================== このチャンネルでは、算数・数学の良問や面白い問題を完全オリジナル解説で紹介しています。 やっています。 また、なぞなぞや漢字クイズ、雑学クイズなど、楽しいクイズもいろいろ掲載。[Click here for channel registration]BGM素材:YouTubeオーディオライブラリ 背景映像素材:原画素材:イラストAC[WEB site]ネタ事実[Twitter]世界のファンシー
算数 面積 問題 難しいに関する情報に関連するいくつかの画像
視聴している【受験算数の面積問題】発想力が問われるちょっと難しい図形の問題!に関する情報を見つけることに加えて、csmetrics.orgが継続的に下に投稿した情報を調べることができます。
算数 面積 問題 難しいに関連する提案
#受験算数の面積問題発想力が問われるちょっと難しい図形の問題。
ファンシーワールド,UCRwFJZWyzlsU3Q7J8BmI5GQ,脳トレ,クイズ,算数問題,面積,良問。
【受験算数の面積問題】発想力が問われるちょっと難しい図形の問題!。
算数 面積 問題 難しい。
算数 面積 問題 難しいの知識がComputer Science Metrics更新されることで、より新しい情報と知識が得られるのに役立つことを願っています。。 csmetrics.orgの算数 面積 問題 難しいに関する情報を見てくれたことに心から感謝します。

三平方の定理そのもの及び根号を用いない解法。
といってもその解法は、三平方の定理を証明する代数的解法又は台形法に準ずる。
AB=a,AF=b,BF=c とする。
2△BFE=c^2=4*8=32
(a-b)^2=c^2-2ab=4^2 ∴2ab=16
四角形ABEDの面積S=1/2(a+b)^2 2S=(a+b)^2=c^2+2ab=32+16=48
従って、S=24
Sir can you please give subtitles in English
中学知識使わないと無理だーーww
(次のように進めました。)求める面積Sのうち、簡単に求まるのは△BEF=8×4÷2=16。残りの、問題となる△ABFと△DFE(≡△ABF)については、次のように求めていきました。まず、AF=x、AB=yとし、△ABFを4枚用意する。次に、一辺の長さがBFとなる正方形(対角線の長さが4×2=8)の各辺(×4)に、△ABFの各辺BF(×4)を張り合わせ、その各点A(×4)を内側に、それぞれが重ならないように配置していくと、中心部分に一片の長さ4の正方形が出来上がる(∵y-x=4)。一片の長さBFの正方形の面積を考えて、8×8÷2=(4×4)+(xy÷2)×4、xy=8。ゆえにS=△BEF+△ABF×2=16+(xy÷2)×2=16+8=24。
平方根なしだと大変 アリだと楽
△BCEは1:2:√3の直角三角形なので
BC=4√3
△ABF≡△DFEより
AB+DE=FD+AF=BC=4√3
台形ABEDの面積は
(AB+DE)*BC/2=4√3*4√3 /2
=24
BC=4√3
長方形だから、AF+FD=4√3
△ABF∽△DEFだから
AB+DE=FD+AF=4√3
S=AD×(AB+DE)/2
=4√3*4√3/2
=24
これを算数で解けるのは天才やろ。
中学生なら有名角使って 4√3*4√3÷2=24 暗算レベル
問題とは関係ないけど走行動画福岡県やん
四角形ABEDの面積は、辺AD=BCを一辺とする正方形の面積の半分だから、BC×BC÷2。BCが分かれば一発なんだが、√を使わないとなると困るな。
受験算数うけるレベルの子なら、頂角30度の二等辺三角形の面積は 等辺×等辺÷4 は既知のものとして使うかな。
定番の考え方を単純に組み合わせた問題です。
斜辺の長さだけ分かってる直角二等辺三角形の面積+頂角が15の直角三角形×2
小学生でできるやつ強過ぎるでw
△BAF ≡ △FDE
AF + FD = BC = 4√3
S(□ABED) = (1/2)(AB + DE)(AD) = (1/2)(DF + AF)(AD) = (1/2)(AD)² = 24
なぜBF:FNが2:1になるのかがわかりません…
√を使ってやっと解けました。小学生でこれを解けたら、凄い。
∠BADに直角の印がないから無理なのでは?(細かいこと言ってすみません)
FB:HM=2:1
ほぼパズルです\_(・ω・`)
動画と同様にFからBEに垂線を引き点Hをとる。
そうすると、動画中の解説図も参考に□AFHBと□DEHFは合同な四角形となります。
ここで、□AFHBを4つ分用意し、1辺が8cmの正方形を作ります。
例えばそのうちの2つを□AFHBと□A'F'H'B'とするなら、FとB'が一致し、AFとA'B'をくっつけ、H'BFHが正方形の一辺となるようにくっつける。
そうすると、1辺が8cmの正方形の中心に、1辺が4cmの正方形の穴が開いたような図形となります。
求める面積は□AFHB2つ分なので、(8*8-4*4)/2=24㎠
\(^O^)/