記事のトピックは三角形 角度 辺 の 長 さを中心に展開します。 三角形 角度 辺 の 長 さを探しているなら、この15度直角三角形の斜辺の長さの記事でこの三角形 角度 辺 の 長 さについてComputerScienceMetricsを明確にしましょう。
目次
15度直角三角形の斜辺の長さの三角形 角度 辺 の 長 さに関連するコンテンツの概要最も正確
このComputerScienceMetrics Webサイトでは、三角形 角度 辺 の 長 さ以外の知識を追加して、より価値のあるデータを自分で持っています。 ウェブサイトComputerScienceMetricsで、私たちはあなたのために毎日毎日常に新しいコンテンツを更新します、 あなたに最も詳細な価値をもたらしたいという願望を持って。 ユーザーがインターネット上のニュースをできるだけ早くキャプチャできるのを支援する。
三角形 角度 辺 の 長 さに関連する情報
高校で習う数学を使わずに、中学校の範囲内で15°の直角三角形の3辺の比を求める方法(の1つ)です。 ・ピタゴラスの定理を使えばいいと思っている人が多いので、タイトル画面を作り直しました。 (2+√3を消す) 2021/3/4
三角形 角度 辺 の 長 さのトピックに関連するいくつかの写真
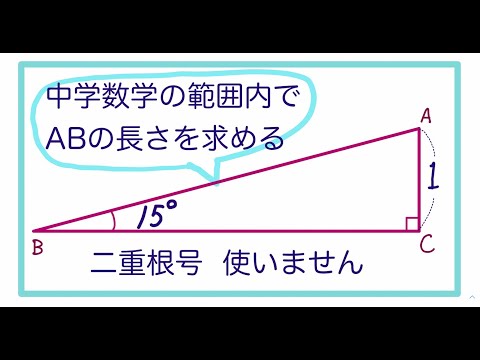
表示している15度直角三角形の斜辺の長さのコンテンツを追跡することに加えて、Computer Science Metricsを毎日下に投稿する他の多くの記事を調べることができます。
三角形 角度 辺 の 長 さに関連するキーワード
#15度直角三角形の斜辺の長さ。
中学数学,三平方の定理,ピタゴラスの定理,15度,直角三角形,三辺の比,三角比,sin15°。
15度直角三角形の斜辺の長さ。
三角形 角度 辺 の 長 さ。
三角形 角度 辺 の 長 さについての情報を使用して、Computer Science Metricsがあなたがより多くの情報と新しい知識を持っているのを助けることを願っています。。 csmetrics.orgの三角形 角度 辺 の 長 さの内容を見てくれてありがとう。

2022年の中央大学の問題でこの先端が7.5°の似たような難問があったわ。
8+2√12=(√2+√6)の二乗じゃいけないの?
自分は二重根号の方で答えました。(この根号は外せないと思いますが)
加法定理が恋しくなる動画だなあ
2つ目のパターンのDから15°の角度で伸ばした線とABの交点をEとすると、△BDEも△ADEも二等辺三角形になり、BE=√2、EA=√6(=2×√2×√3/2)となるので、その合計は√2+√6となる。
大人になると定規ではかります 無意味な勉強だよね
これは美しい解き方ですね。
二重根号も三角比も高校の学習内容なので使わない解答なると難しかったです。
相似で立式したら二重根号で詰みました。
こういう操作を一度学習した生徒はその後の図形の問題も美しく解くのでしょうね。
説明が計算を隠し非常に解りにくい
大変失礼ですがこんな解き方は教えません。1辺2+√3の正方形にこの直角三角形を2つ書いて中に正三角形を作ってください。瞬殺です。
補助線の引き方で明暗が分かれるね。要は、30°、60°、90°と45°、45°、90°の三角形を上手く作図することが重要ってことか。
ん???
三角形ADCの3辺比が1:2:√3っていうのは、中学校で習うんだっけ?
なんか、三角関数を習った時に一緒に習った覚えしかないんだけど。
それとも、地域によって違うのかね?
加法定理使ったら瞬殺レベルなんだけど、高校数学だったっけ?
こんなのとけて何か意味があるんですかね?1/cos75でいいんじゃない
別解ですが、
①3:18~と同じように、BCに対して△ABCと線対称となるような三角形を書き、Aと対象な点をEとする。
②BE上に、AE=APとなるような点Pをとる。この時、△APEは二等辺三角形なのでAE=AP=2、∠AEP=∠APE=75度となる。
③点PからABに垂線を書き、ABと交わる点をQとする。
④この時、△QPAは直角二等辺三角形になるのでAQ:AP=1:√2、AP=2なのでAQ=√2、PQ=√2となる。
⑤△BPQに注目すると、鋭角が30度と60度の直角三角形なので、BQ=PQ×√3=√2×√3=√6となる。
⑥従って、AB=AQ+BQ=√2+√6
というような解き方もありますね。
最初はどんなやり方で答えを出しても良いと思いますが、その結果に√2+√6という答えを見たら、そこで終わってしまうのではなく、
ABを√2:√6に分割する点に、図形的にどんな意味があるのか、と考えてみると良いかもですね。
二重根号を外すために因数分解するのね
上にBCを1辺とする正方形を作ってその中にACを1辺とする正三角形作ったらいけた
この問題は余弦定理も使っちゃいけない?
補助線とか、(値としては同じだけど、なぜ、それに)置き換えるとか、
同じ数を足して引いても元と同じ値、a+b=1なら(a+b)を掛けても同じ値、…
といった類を使わず解くのは、(原理的に)無理なんだろうかと、思ったなぁ。昔。
この方法を発見するより、(√2+√6)^2=8+4√3を発見するほうが早い気がしないでもない
頭のもやもやがとけた(^o^)
ちょっと違うけど
45度の補助線とBCとの交点をDとして、そのまま伸ばして△ABD相似△CEDとなるように三角形を作る。この時AD=√2、CD=1なんで相似比は√2:1
BD=1+√3、ED=xとして相似比からED=x=1+√3/√2(分母の√2は全体にかかってます)
ここでEからBCに推薦を下ろし、その交点をFとする。△FEDは直角二等辺三角形なのでEDの値よりEF=1+√3/2(分母の2は全体にかかってます)
ここで△EFCは角C=30度、角F=90度の三角形であるのでEF:EC=1:2=1+√3/2:yだから
EC=y=1+√3
ここでAB:EC=√2:1=z:1+√3より
AB=√2+√6 (証明終了)
Eは動画のものとは全くの別物です。
大分わかりにくいと思うからそこのところはすみません。ただ書いたらわかると思います。
このやり方は同一円周上からの方べきでできないかなぁと思ったら浮かんできました。
斜辺は絶対に.2、です、2の相似比で。単位円、1、の証明は難しいです。
二重根号出たら今度から2乗してから因数分解して戻してみよう
武田鉄矢の声かと思いました
自分的にはAからBEに垂線をおろしたらその垂線の長さはABの半分なので、そこから相似比を使って求める方が分かり易いかな
マウントとかじゃなくて、中高一貫やと中学生に教える時とかもどこまでが中学範囲かわからんくて困るw
2 √(2 + √3) を正解にしないなら数学の敗北
DからABに垂線下ろしたくなるわぁ
三角形ABCと合同の三角形ACEを作った後、半直線BAと辺BEに垂直な直線lを頂点Eから引いて、
半直線BAとの交点をDとして、30度、60度、90度の直角三角形BDEとACEを作って解きました。