記事のトピックは内 接 円 の 半径 求め 方を中心に展開します。 内 接 円 の 半径 求め 方について学んでいる場合は、csmetrics.orgこの記事【中学受験】内接円の半径を5秒で求める裏技!塾のテクニックを無料公開してごめんなさい。で内 接 円 の 半径 求め 方について学びましょう。
目次
【中学受験】内接円の半径を5秒で求める裏技!塾のテクニックを無料公開してごめんなさい。の内 接 円 の 半径 求め 方に関連する情報の概要
このcsmetrics.org Webサイトでは、内 接 円 の 半径 求め 方以外の他の情報を追加して、自分自身により価値のある理解を深めることができます。 ウェブサイトComputer Science Metricsで、私たちはあなたのために毎日毎日常に新しい情報を公開します、 あなたに最高の知識を提供したいという願望を持って。 ユーザーが最も正確な方法でインターネット上に情報を追加できます。
トピックに関連するいくつかの情報内 接 円 の 半径 求め 方
#中学受験 #内接円の半径 塾のテクニックを知っていれば内接円の半径は暗算で計算できます。 受験算数、中学数学が出題されます。 算術予備校 モッティさんは、昼間は中学・高校で数学を教え、夜は学習塾で数学を教えています。 算数は楽しい! をモットーに、アクティブで楽しい授業を行っています。 2021年春、YouTubeで配信を始めました。 中学受験を控えた小学生の皆さんを全力で応援します。 noteで入試解説を真面目に書いています。 ☆チャンネル登録 ☆note 入試問題解説 note ☆twitter(お仕事依頼はTwitterのDMで)
内 接 円 の 半径 求め 方の内容に関連する画像
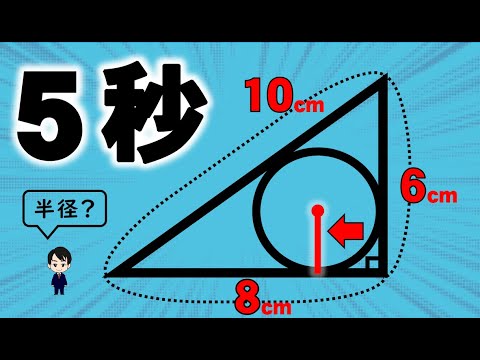
視聴している【中学受験】内接円の半径を5秒で求める裏技!塾のテクニックを無料公開してごめんなさい。に関するコンテンツを読むことに加えて、csmetrics.orgが継続的に下に投稿した他のコンテンツを見つけることができます。
一部のキーワードは内 接 円 の 半径 求め 方に関連しています
#中学受験内接円の半径を5秒で求める裏技塾のテクニックを無料公開してごめんなさい。
内接円の半径,裏技,中学受験,内接円。
【中学受験】内接円の半径を5秒で求める裏技!塾のテクニックを無料公開してごめんなさい。。
内 接 円 の 半径 求め 方。
内 接 円 の 半径 求め 方の内容により、ComputerScienceMetricsが提供することを願っています。これがあなたにとって有用であることを期待して、より新しい情報と知識を持っていることを願っています。。 csmetrics.orgの内 接 円 の 半径 求め 方についての知識をご覧いただきありがとうございます。

ヘロンの公式と内接円の公式使ってもいける?
順にやってもそんなに時間かからない。
半径+あ=6
半径+い=8
あ+2=い
あ+い=10
あ+あ+2=10
あ=4
半径=6-4=2cm
一応同じ解法でしたが、事実上、一次方程式を解いているので、算数の範囲内と言えるのか疑問です。
あと345の内接円の半径が1である事実や、直角三角形の内接円の直径が長辺+短辺-斜辺であることから解答することもできますが、すべての算数の教科書に載っているとは思えず、使うなら証明を添えなければ減点される可能性があります。その証明も上記の方程式しか思いつかないので、やはり算数の範囲とは言えないかもしれません。
6X8=48
48÷(10+8+6)=2
x+(6-x)=6 x+(8-x)=8
(6-x)+(8-x)=10 14-2x=10 2x=4 x=2
3:4:5 3+4-5=2 r=1
5:12:13 5+12-13=4 r=2
7:24:25 7+24-25=6 r=3
8:15:17 8+15-17=6 r=3
Don't think. Feel !
直角三角形に内接する円の直径=斜辺以外の辺の長さの合計-斜辺の長さ
学生のころは準公式だと思ってました
この場合6+8-10=4
よって半径は2
小学生が、円の接線の性質(外接線の法則)なんか、習ったっけ。中学生からじぁなかったかな~
3:4:5の直角三角形の内接円の半径は1
辺の比が2倍だから半径も2倍の2
知ってれば1秒です
大手塾の生徒なら大抵知っているはず
とっても面白いやり方ですね。感動したニャア~simple is best・・